Translation using deep neural networks - RNN (part 1)
In this article, I’ll introduce language modeling using deep learning and will focus on the problem of translation.
I’ll cover how language was modeled using deep learning prior to transformers, which was by using recurrent neural networks (RNNs).
I’ll compare (Bahdanau et al., 2015) which introduces the idea of attention in RNNs, with a paper published around the same time (Sutskever et al., 2014) which does not use attention. I’ll explain in detail what attention is and why it was introduced, as well as try to reproduce the results from these papers. The results from these papers are actually contradictory; (Sutskever et al., 2014) reported better performance than (Bahdanau et al., 2015), however the latter is well known and influential for introducing attention. This is surprising to me, and shows that researchers found the idea of attention to be useful regardless of the performance reported in these papers.
In the section Sequence to sequence models, I’ll give background on how to model problems where we take a sequence as input and output a sequence, with special attention (no pun intended) to the problem of translation. In Experiments and results I’ll reproduce (Sutskever et al., 2014) and (Bahdanau et al., 2015). And in Implementation details I’ll cover technical details about how the models were implemented.
All code for this article is available here.
In the next article I’ll cover how language is modeled today using transformers.
Introduction
Avoiding NLP
In school, I always skipped over the natural language processing (NLP) topic for several reasons
NLP used to be boring to me and language-specific where linguistics domain knowledge was needed. It involved steps such as
- tokenization (which is still needed but there wasn’t as good support for it before and it is annoying to implement),
- parts of speech tagging
- entities extraction
- …, etc
The second reason why I avoided this topic is that I didn’t see much practical value in learning NLP. When would I ever need to build a chatbot or translation model?
These reasons lead to me cringing everytime I saw “NLP” mentioned
Language modeling today
Turn to 2024 and language modeling is arguably the hottest topic in AI, so much so in fact that when some people say “AI” they are actually referring to language modeling.
The models used for language modeling are also general purpose models that can handle any problem in which the data can be broken up into a finite sequence of tokens such as image understanding/generation, audio, biology (genomics), etc, and so language is just one use case of these models.
What is a language model?
Simply put a language model is a model that has learned to predict the next token given the previous tokens. The token is usually a word/subword/single character, but can be any discrete chunk of data that is part of a fixed vocabulary.
What is a large language model?
A large language model or LLM is a language model that has been trained on a ton of text and has many parameters (billions or trillions). Parameters are akin to the weights in biological neurons which determine whether they fire or not.
Why is language modeling now relevant and interesting?
Language models are part of a trend in AI of generative models. Generative models produce data, whereas historically machine learning models used to only predict a single variable, such as whether a review was good or the price of a house.
Other types of generative models would cover the tasks of image generation, video generation, audio generation, and other kinds of generation. But this article will focus on language modeling.
It is an understatement to say that generative models are a hot topic right now (mostly language models). It seems overnight companies are racing to build bigger and better models and other companies are racing to incorporate these models into their product offering. Schools are discussing whether to allow the use of LLMs or how to even prevent them from being used.
We’ve seen that GPT-3.5+ models are incredibly powerful. They have seemingly limitless knowledge about seemingly all topics and can create and combine things in novel ways. When GPT-3.5 came out, most people discovered that it can write haikus, breaking news articles about falling leaves, and get it to say other amusing and funny things.
But language models are more than just haiku-generating machines. I frequently use GPT to figure out confusing things in code or an API I’m unfamiliar with, or to do tedius software engineering related things. I also find myself bouncing ideas off of GPT to get unstuck.
There is also tremendous potential in teaching and education. While reading a book or watching a video, you can ask GPT to explain something to better understand it; this makes learning more interactive and effective.
In research, many people are doing and have been doing amazing research. There is not even close to being enough time for anyone to keep up. Large language models can help surface and summarize research and help people navigate the idea landscape.
Much of life can be tedious or confusing; large language models can hopefully serve as the “all knowing” guide and enhance our creativity and insight without us needing to sacrifice our autonomy or intelligence.
Sequence to sequence translation
Translation has historically been a challenging task to automate and was used as a springboard for different AI research.
I chose translation as the task to focus on for learning language modeling as 2 seminal papers in language modeling, which I’ll get to, also used translation as the task.
The task of translation, as you may have guessed, involves translating an arbitrary document (word, sentence, paragraph, whatever) from 1 language into another.
Why is translation using neural networks difficult
Translation using neural network models is challenging for several reasons.
Language involves sequences of arbitrary length
According to (Sutskever et al., 2014)
Despite their flexibility and power, DNNs [Deep Neural Nets] can only be applied to problems whose inputs and targets can be sensibly encoded with vectors of fixed dimensionality. It is a significant limitation, since many important problems are best expressed with sequences whose lengths are not known a-priori.
Today, this issue seems like a non-issue. But back in 2014 this was seen as a novel problem to solve.
Traditional machine learning operates on fixed length vectors, such as variables representing imporant features of a house (e.g. # of bedrooms, square footage, location, etc), the length of which is known in advance.
Language is different in that sentences can be of arbitrary length. How to encode the sentences “I ate a cheese sandwhich” as well as “It is morning.” such that the model receives a fixed length input?
Long inputs
The paragraph
It was cold outside so I wanted something warm to drink. I was out of tea so I thought to go to the store to buy some. My favorite kind of tea is matcha tea because of its health benefits. It was on sale so I bought some matcha tea. Drinking the tea really warms me up and gives me energy!
contains a lot of information. How do we encode all this information so that we can know how to translate it?
In fact, early models would do better at shorter sentences than longer ones because of this issue. The model was able to encode the meaning only for very short inputs but tended to not properly capture longer inputs.
(Cho et al., 2014) analysis of early DNN translation models states:
Our analysis shows that the performance of the neural machine translation model degrades quickly as the length of a source sentence increases.
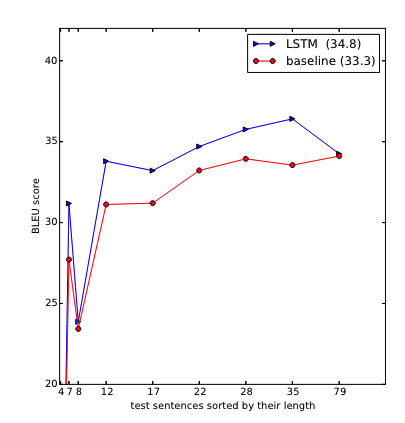
However, (Sutskever et al., 2014) states
We were surprised to discover that the LSTM did well on long sentences
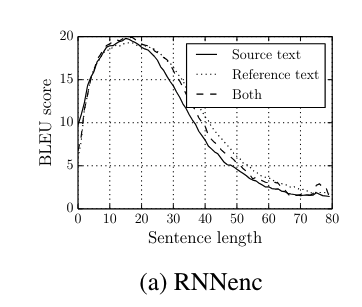
And then again in the seminal paper (Bahdanau et al., 2015), which I’ll discuss in more detail later shows the same problem, that the model struggles with longer sentences:
Notice how the performance (BLEU score, I’ll discuss in more detail in the section Measuring performance of translation tasks: BLEU score) degrades rapidly as the sentence length increases in the RNNenc-50 and RNNenc-30 models.
So there is a discrepancy among these papers when discussing the problem of sentence length. Sutskever et al, 2014 say that the model performs well on long inputs, but Cho et al, 2014 and Bahdanau et al, 2014 say that the models are defficient when the input size increases. All these papers use the same dataset, WMT ‘14 for training and evaluation.
The problem of sentence length would lead to the idea of attention in Bahdanau et al, 2014, which forms the basis for the transformer architecture.
Vocabularies are large
In language models, we have to turn the text into a series of tokens. Tokens are the smallest unit of input when using deep neural network models to model language.
The vocabulary is then the set of possible tokens. We could just use single characters as the set of tokens, which would require a small vocabulary. However using single characters poses other difficulties as it would increase the input/output size if every character was modeled separately. We would like something flexible enough to handle individual characters as the smallest token, up to entire phrases. See (Radford et al., 2019) for this discussion.
Vocabularies are large. According to the website open source Shakespeare there are 28,829 unique words in all of Shakespeare’s works, and apparently 40% of those words are used only once. That is a lot of words, but relatively modern LLMs (e.g. GPT2) use a token size of ~50,000 (Radford et al., 2019), since these models need to understand more than just the vocabulary of Shakespeare.
Large vocabulary sizes pose some challenges. The first is that once the data is tokenized, we typically will construct a vector of real numbers, as this is easier to model than simply providing an index. This vector is called an embedding vector and the set of embedding vectors for all tokens in the vocabulary the embedding matrix. A large vocabulary size means a large embedding matrix.
Another challenge with a large vocabulary size is that when we predict each token at the decoding step, we typically use a linear transformation, which requires hidden \(\times\) number of tokens weights, which increases compute. For example if the hidden size in the decoder is \(1000\) and the number of tokens is \(30000\) then we would require \(1000 \times 30000 = 3e7\) weights (multiplications/additons) in this layer alone.
Large vocabulary sizes also mean that we need a very large dataset in order to capture enough examples for every token in the vocabulary in order to train each token sufficiently. For example rarer tokens might be undertrained.
Translation is difficult
The Hebrew sentence יש לי גרביים means “I have socks”.
The literal translation is “There is to me socks”. This means that a language model cannot just learn a mapping between words. If the model needed to translate the english sentence “I have socks” to Hebrew, it cannot just look up the Hebrew word for “I”, which would be “אני”. It needs to know that the 2 words “I” followed by “have” get translated to the Hebrew “יש לי”. On the other hand if the sentence were “I am a man”, then “I” should get translated to “אני”.
Another example would be translating the phrase “black cat” into spanish in which case it is “gato negro”. In other words when the model sees “black” it should output “gato” or “cat” and when it sees “cat” it should output “negro” or “black”.
This is just scratching the surface as to why translation is difficult.
Sequence to sequence models
Translation involves taking in a sequence of text and producing a sequence of text. For example:
Input:
יש לי גרביים
Output:
I have socks.
The way that we (humans) process language is by starting from the beginning and reading until the end.
I—have—socks—.
We mentally break up the sentence into chunks and process it sequentially in parts. We also need to understand the meaning of the sentence as a whole.
When translating this sentence into a different language, after we mentally process the input, we then start producing the output one chunk at a time.
יש—לי—גרביים
So this involves 3 main steps:
- tokenize the input into a sequence of tokens
- process and condense/understand the input so that we can translate it
- use the condensed form from (2) to produce a translation token by token
We would like a machine learning model that can do steps (2) and (3) above.
The encoder-decoder architecture as proposed by(Sutskever et al., 2014) does just this.
The encoder processes and compresses the input into a meaningful representation, a fixed length vector. The decoder then takes this meaningful representation and then generates the output 1 token at a time.
In (Sutskever et al., 2014) both the encoder and decoder are RNNs, (or more specifically a variant called LSTM). Let’s take a look at how an RNN works.
RNNs
The basic form of an RNN is the following, in pseudo-code:
class VanillaRNN:
def forward(self):
h_t = self.inital_state
outs = []
for x_t in seq:
h_t = f(h_t, x_t)
outs.append(h_t)
return outs, h_t
In words, we initialize a “hidden state” or \(h_t\) of the RNN to the current state. We loop over every token in the input. For each token we calculate a function called \(f\) which takes as input the current token \(x_t\) as well as the current state \(h_t\). We append the current hidden state for timestep \(t\) to the list of outputs outs.
In math, \(f\) takes a specific form.
\[h_t = f(h_t, x_t; W) = tanh(W_{hh}h_t + W_{xh}x_t + b_h)\]The hidden state, \(h_t\) is what stores the compressed/meaningful representation of the sequence. Let’s look at how the hidden state is calculated.
There are 2 weight matrices involved:
\[W_{hh}\in \mathbb{R}^{h \times h}\] \[W_{xh}\in \mathbb{R}^{x \times h}\]as you can see \(W_{hh}\) is multiplied with \(h_t\), \(W_{xh}\) is multiplied with \(x_t\) and the 2 resulting vectors are added along with a bias.
The resulting vector is then passed through the a function \(tanh\) which is just a function that maps \((-\infty, +\infty) \to (-1, 1)\). It looks like this:

that means that the hidden state is a vector \(h_t \in \mathbb{R}^h\) where each element is between \((-1, 1\))
example
Let’s look at a simple example using the sentence “I have socks.” as input, and pass it through the vanilla RNN.
Let’s tokenize the sentence as [“I”, “have”, “socks”, “.”]
Let the embedding vector be \(x \in \mathbb{R}^2\)
Let the hidden state be \(h \in \mathbb{R}^3\).
What has happened here?
First we split up the sequence “I have socks.” into tokens “I”, “have”, “socks”, “.”
Then we mapped each token to a unique number using the variable vocab to map between token and number.
For each token id we looked up an embedding vector. The embedding vector is a fixed length numeric vector and is a way to map each token to a vector of numbers, since the neural network can only take numeric values as input. It starts out randomly initialized and is learned during training.
Mapping the sequence of tokens into a sequence of vectors gives us:
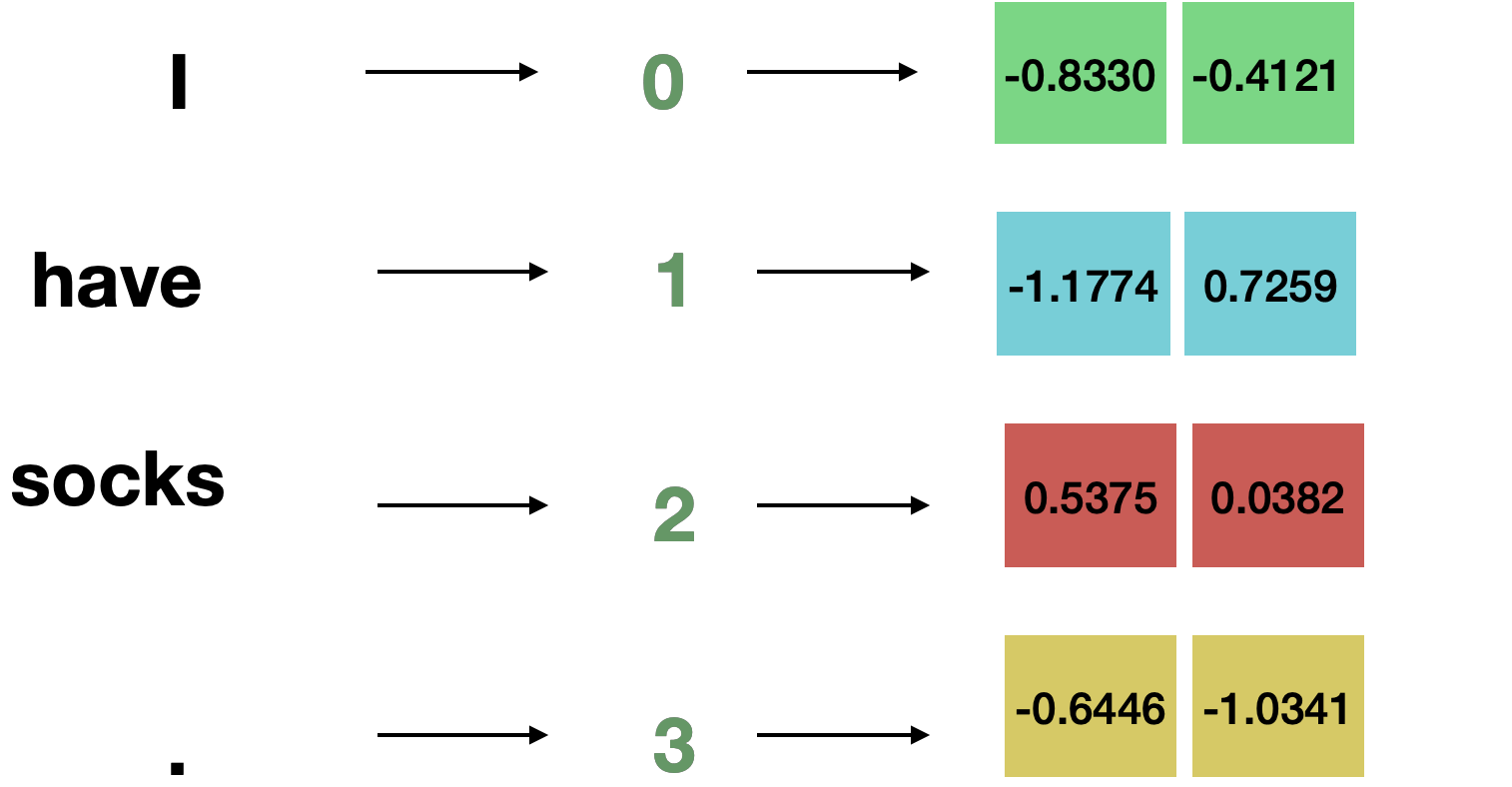
We initialized the hidden state \(h_0 = \begin{bmatrix} 0 & 0 & 0 \end{bmatrix}\)
then we iterated over each token, and updated the hidden state for each token.
In detail:
- extract embedding vector for token “I”, \(x_1\), and update hidden state \(h_1\)
- extract embedding vector for token “have”, \(x_2\), and update hidden state \(h_2\)
- extract embedding vector for token “socks”, \(x_3\), and update hidden state \(h_3\)
- extract embedding vector for token “.”, \(x_4\), and update hidden state \(h_4\)
After all this math, we get a final hidden state \(h_4\) and an output \(o\) which includes \(h_t\) for each timestep \(t\)
\[h_4 = \begin{bmatrix}-0.2049 & 0.3322 & 0.3161\end{bmatrix}\] \[o = \begin{bmatrix}-0.3126 & 0.5246 & 0.6447\\0.0277 & 0.3934 & 0.8409\\-0.8055 & -0.0275 & 0.0972\\-0.2049 & 0.3322 & 0.3161\end{bmatrix}\]What do these numbers represent? The final hidden state \(h_4\) represents the RNN’s compressed/useful representation of the input sequence I have socks.. The outputs \(o_t\) represent the compressed/useful representation after processing token \(t\) and having processed the previous \(t-1\) tokens.
The hidden state is reset to \(0\) each time it processes a new sequence.
Why “recurrent” neural network
Why are RNNs called “recurrent” neural networks?
The name “recurrent” in “recurrent neural network” comes from the fact that the hidden state \(h_{t-1}\) is recursively used to calculate the new hidden state \(h_t\)
If we unpack a single update of \(\textcolor{blue}{h_t}\), we get:
\[\textcolor{blue}{h_t = tanh(W_{hh}\textcolor{lime}{h_{t-1}} + W_{xh}x_t + b_{hh} + b_{xh})}\]if we unpack \(\textcolor{lime}{h_{t-1}}\) we get:
\[\textcolor{lime}{h_{t-1} = tanh(W_{hh}\textcolor{orange}{h_{t-2}} + W_{xh}x_{t-1} + b_{hh} + b_{xh})}\]Plugging this into the previous equation, we get:
\[\textcolor{blue}{h_t = tanh(W_{hh}(}\textcolor{lime}{tanh(W_{hh}\textcolor{orange}{h_{t-2}} + W_{xh}x_{t-1} + b_{hh} + b_{xh})}\textcolor{blue}{) + W_{xh}x_t + b_{hh} + b_{xh})}\]If we unpack this for one more timestep, \(\textcolor{orange}{h_{t-2}}\) would be \(\textcolor{orange}{h_{t-2} = tanh(W_{hh}h_{t-3} + W_{xh}x_{t-2} + b_{hh} + b_{xh})}\)
Plugging in \(\textcolor{orange}{h_{t-2}}\) we get:
\[\textcolor{blue}{h_t = tanh(W_{hh}(}\textcolor{lime}{tanh(W_{hh}(}\textcolor{orange}{tanh(W_{hh}h_{t-3} + W_{xh}x_{t-2} + b_{hh} + b_{xh})}\textcolor{lime}{) + W_{xh}x_{t-1} + b_{hh} + b_{xh})}\textcolor{blue}{) + W_{xh}x_t + b_{hh} + b_{xh})}\]The full recursive equation would be:
\[h_t = tanh(W_{hh}(tanh(W_{hh}(...tanh(W_{hh}h_0 + W_{xh}x_1 + b_{hh} + b_{xh})...) + W_{xh}x_{t-1} + b_{hh} + b_{xh})) + W_{xh}x_t + b_{hh} + b_{xh})\]- The calculation of the hidden state \(\textcolor{blue}{h_t}\) involves the previous \(t-1\) hidden states \(\textcolor{lime}{h_{t-1}}, \textcolor{orange}{h_{t-2}}, ... h_{0}\)
- The hidden state calculation \(\textcolor{blue}{h_t}\) involves each of the previous \(t-1\) tokens in the sequence \(\textcolor{lime}{x_{t-1}}, \textcolor{orange}{x_{t-2}}, ... x_{0}\). This enables the model to “see” the entire sequence.
- The weights and biases \(W_{hh}\), \(W_{xh}\), \(b_{hh}\), \(b_{xh}\) are used repeatedly when processing the sequence for each hidden state \(h_t\)
- There are a lot of matrix-matrix multiplications (\(\textcolor{blue}{W_{hh}} * \textcolor{lime}{W_{hh}} * \textcolor{orange}{W_{hh}}\)). This can lead to very large numbers (exploding gradients) or very small numbers (vanishing gradients)
Note: This is showing the forward pass of a simple RNN using a single training example. The model would actually be trained on many examples, and the model parameters \(W_{hh}\), \(W_{xh}\), \(b_{hh}\), \(b_{xh}\) would be trained using backpropagation.
More complicated architectures
There are various issues with this simple “vanilla RNN” architecture that people have worked on addressing over the years, and there are other improvements to increase complexity and expressiveness.
Mentioned above is the issue that because there are many matrix-matrix multiplications, the simple RNN has the issue of vanishing and exploding gradients which prevent the network from learning well. People have worked on addressing this issue by introducing LSTM and GRU and these variants are used in practice instead of the simple RNN. These fix the issue of vanishing gradients; exploding gradients are usually handled by thresholding the gradients if the norm is larger than a certain value.
To increase the model expressiveness, you can stack multiple RNNs together where the output from 1 is given as the input to the next. Set num_layers argument >1 in pytorch to do this.
It might also be useful to process a sequence in the forwards direction and in the backwards direction. To do this, you can use 2 RNNs: 1 that processes the sequence forwards and the other backwards. Set bidirectional=True in pytorch to do this.
Encoder-decoder architecture
So far we’ve discussed how an RNN can be used to process the source sequence. What about translation? To do translation, we have to add an additional step.
The proposed architecture is the so-called encoder-decoder architecture. The idea is that an RNN processes the input sequence, as we’ve shown above. Then another RNN, the “decoder”, takes the hidden state of the “encoder” RNN as input and tries to predict the correct translated token at each timestep. From (Cho et al., 2014):
The proposed neural network architecture, which we will refer to as an RNN Encoder–Decoder, consists of two recurrent neural networks (RNN) that act as an encoder and a decoder pair. The encoder maps a variable-length source sequence to a fixed-length vector, and the decoder maps the vector representation back to a variable-length target sequence. The two networks are trained jointly to maximize the conditional probability of the target sequence given a source sequence.
Here is a picture of what that would look like for the sequence “I have socks.” -> יש לי גרביים
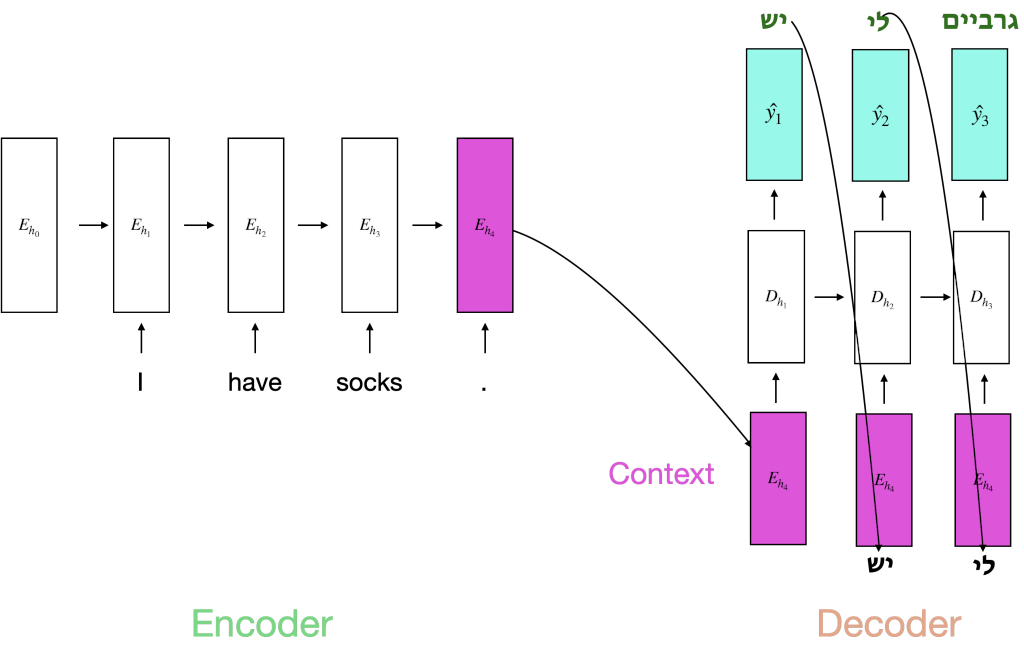
You’ll notice a few things from this picture of the encoder-decoder architecture for translation.
- The encoder and decoder look similar. They are both separate RNNs that are connected to each other and trained together. Each have separate hidden states.
- The inputs to each timestep \(t\) in the decoder are the context vector as well as the previous token.
- The context vector is the last hidden state \(h_t\) in the encoder (the encoder’s representation after processing the entire input sequence). The same context vector is used for each timestep \(t\) in the decoder
- At each step in the decoder we predict the correct token \(\hat{y_{t}}\) and compare it with the correct token at that timestep
Note: \(\hat{y_{t}}\) is calculated using the softmax function over every possible token in the target vocabulary. For example, if there are 10,000 possible tokens in the target language vocabulary, then \(\hat{y_{t}}\) will be of size 10,000. We then calculate \(argmax\) over this vector to choose the most confident token at that timestep.
Note: both the encoder and decoder networks are trained end-to-end using backpropagation using the cross-entropy loss function
Note: At inference time we use the previously predicted token \(\hat{y}_{t-1}\) rather than the truly correct token at each timestep \(t\)
attention
You might have noticed that the entire input sequence is compressed into what is called the context vector. The decoder must rely on all of the meaning of the input sequence being encoded into the context vector in order to produce the translation.
In the example sentence
I have socks.
it might be possible to properly represent this in a fixed length vector.
But what if the sentence was
I have socks that are thick and made of wool because it is cold outside; it is comfortable to wear around the house while I look outside at the white snow gently falling to the ground.
It might be difficult to encode all of the meaning into a fixed length vector representation of numbers so that the decoder can produce a correct translation. It is sort of like the game of “telephone”; the meaning and nuances would be lost in translation.
This is the same pattern that (Cho et al., 2014) observed, see Figure 1
The bleu score on the vertical axis is a measure of translation quality, which I’ll discuss later in the article. Notice how as sentence length increases there is an exponential dropoff in translation quality.
(Bahdanau et al., 2015) addressed this in their now famous paper “NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE”.
This paper is cited as the paper that introduced attention in neural networks. Attention is the backbone of the transformer architecture which is the architecture used to train LLMs, so it’s sort of a big deal.
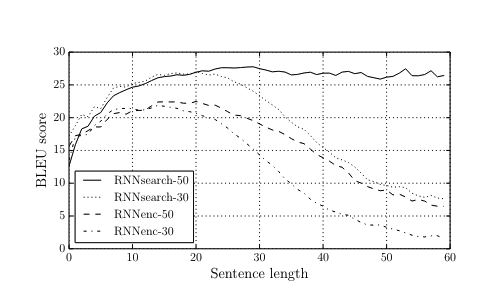
In Figure 3, they compared an encoder-decoder model without attention, as we’ve discussed above, with a model using attention.
RNNenc-* is the same model we looked at before. We can see a similar dropoff in translation quality as the sentence length increases.
Compare this to RNNsearch-* which is a model with attention. Both RNNsearch models have better performance, and interestingly, the RNNsearch-50 model shows no sign of decrease in performance as the sentence length increases.
what is attention?
Attention, as the name implies is giving the model the ability to pay attention to certain parts of the input.
While (Bahdanau et al., 2015) was the paper to popularize the idea of attention, it was refined and simplified in (Vaswani et al., 2017), and the latter is what is typically used. I’ll go over both versions of attention.
Bahdanau (additive) attention
Let \(s_{i-1}\) be the previous hidden state in the decoder
Let \(h_j\) be the hidden state in the last layer of the encoder RNN at each timestep \(j\)
Bahdanau attention adds 3 new parameters:
\[W_a \in \mathbb{R}^{n \times n}\] \[U_a \in \mathbb{R}^{n \times 2n}\] \[v_a \in \mathbb{R}^{n}\]where \(n\) is the hidden state dimensionality in both the encoder and decoder (must be the same) and \(U_a\) is n x 2n because the encoder was bidirectional in the paper.
Then the attention weights \(a\) can be calculated by taking as input the decoder previous hidden state \(s_{i-1}\) and the hidden state in the last layer of the encoder RNN at each timestep \(j\) as:
\[a(s_{i-1}, h_j) = {v_a}^Ttanh(W_as_{i-1} + U_ah_j)\]How does this give the model the ability to pay attention to certain parts of the input?
We are taking the current decoder hidden state \(s_{i-1}\) when processing token at timestep \(i\) and adding it to the hidden state in the encoder at each timestep \(j\) \(h_j\). That is why this form of attention is referred to as “additive” attention.
The result of \(a(s_{i-1}, h_j)\) will be \(\in \mathbb{R}^{t}\) where \(t\) is the number of tokens in the input sequence.
It will look like:

We then map the numbers to a probability distribution using the softmax function. The attention weights will then look like:
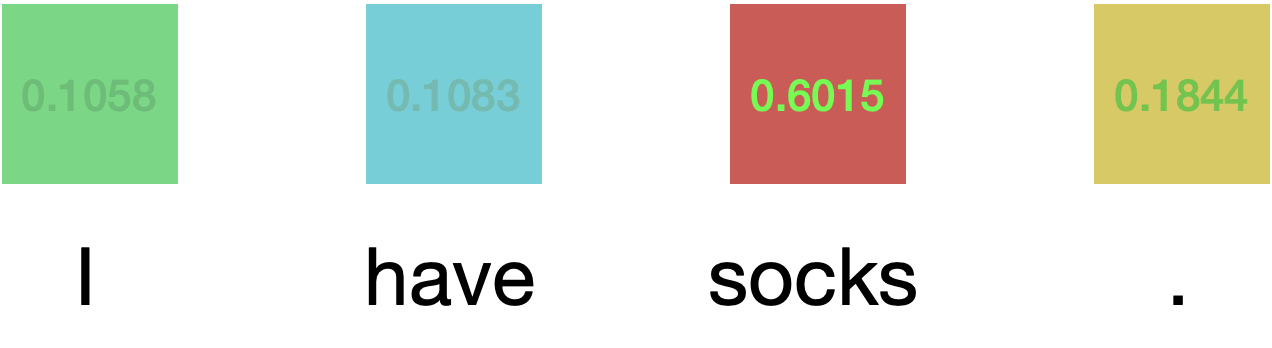
This has the interpretation of “which tokens in the input are most important for outputting the current token in the decoder?”
Note that we use a probability distribution rather than a hard cutoff when determining which tokens are important. Some tokens may be less important than others, but have some importance.
Scaled dot-product attention
When people today refer to “attention” they are generally referring to the scaled dot-product attention rather than the previously discussed additive attention. There are several reasons for this.
You may have noticed that the additive attention is not that straightforward. Why are we adding the decoder hidden state with the encoder hidden state at each timestep?
(Vaswani et al., 2017) in their influential paper “Attention is all you need” reformulate attention to be the following, which is the basis of the transformer architecture.
\[attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V\]This is similar to the previously discussed additive attention but with a few key differences.
The query \(Q\) is the current vector we are asking the question “what should we be paying attention to?”. The keys \(K\) are the set of vectors, or matrix, which are the options to pay attention to. The values \(V\) is the set of vectors, or matrix, that each key maps to.
In the case of translation using the RNN encoder-decoder model, the query \(Q\) is the current decoder hidden state of dimension \(d_q\). The keys are the encoder outputs which get mapped to the dimension \(d_{t \times {d_q}}\) and the values are also the encoder outputs mapped to the dimension \(d_{t \times {d_v}}\)
The idea is that we want to find which keys \(K\) in the input the current query \(Q\) should attend to. This is computed as the dot product between \(Q\) and \(K\). The dot product has the theoretical interpretation as the similarity between 2 vectors.
We are multiplying the query \(Q\) of dimension \(q\) with \(K^T\) of dimension \({q \times t}\). The resulting vector is of dimension \(t\).
This is then divided by \(\sqrt{d_k}\), and hence the name “scaled” in “scaled dot-product” since we are scaling the dot-product by \(\sqrt{d_k}\). The reason for this is given as
We suspect that for large values of \(d_k\), the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients. To counteract this effect, we scale the dot products by \(\sqrt{d_k}\).
We then take the softmax, resulting in a probability for each timestep \(t\).
Finally, we multiply this by the matrix \(V\). The resulting vector is of size \(d_v\) and each element is a weighted sum of importances calculated from the attention weights in the previous step.
How is attention different from the previous encoder-decoder approach?
In Figure 6 we showed an encoder-decoder architecture in which a context vector is passed to each decoding step. We noted that this context vector is computed from the output of the encoder and is the same at every decoding step. We noted that this has the potential problem that the entire input must be encoded into a single meaningful representation.
Attention tries to fix this problem by figuring out what the most relevant bits of the input are for each decoding step. In the example long input that we made up above
I have socks that are thick and made of wool because it is cold outside; it is comfortable to wear around the house while I look outside at the white snow gently falling to the ground.
when we are translating at the end the word “snow”, maybe “socks that are thick and made of wool” is less relevant than “white” and “gently falling”.
In this way the attention mechanism allows us to pay attention to only the relevant parts of the input for each decoding step, and so we don’t have to construct a single meaning of the entire input.
Measuring performance of translation tasks: BLEU score
How do we measure the correctness of a machine-translated output?
We could hire native speakers and/or professional translators to look at and rate the translation qualities. But looking at and judging the quality would take a very long time and be very costly. It also wouldn’t be reproducible if multiple different algorithms should be compared against a benchmark dataset.
Let’s take a stab at a naive translation quality algorithm.
Let’s say the correct translation is
In my dresser I have socks.
but our model outputs
I have socks.
We can see that the model’s output is partially correct. So maybe if we were to score the correctness of the translation we’d like it be be considered partially correct but not completely correct, and not completely incorrect.
If we were to just match up each word with the correct word
In -> I
my -> have
dresser -> socks
We would give this a score of 0, since no word matches up. In fact it is exceedingly rare for 2 translations to match a given translation exactly.
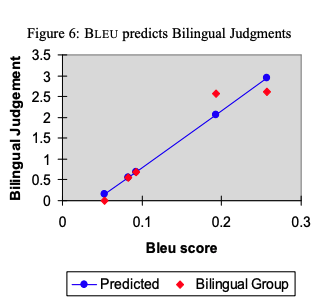
BLEU score is the standard metric used to evaluate translation models. It was proposed in (Papineni et al., 2002). The goal of the BLEU score is to be automated and to correlate with how well a human would judge the translation quality of a given translation to be.
See this interesting figure in the paper in which the authors found the bleu score to correlate with how bilingual humans rated the quality of a translation:
At a high level, the bleu score computes an average of precisions for \(n\)-grams up to a certain \(n\).
Let’s take a look at an example
example
The bleu score for the prediction I have socks. when the reference translation is In my dresser I have socks. is \(0.47\). The bleu score ranges between \([0, 1]\) and so a bleu score of \(0.47\) is decent but not perfect.
Let’s break down the calculation further. We calculate precision scores for \(n\)-grams up to \(n\), in this case 4. Precision is defined as \(\frac{TP}{TP + FP}\), in other words the number of \(n\)-grams that we predict in our translation that are correct.
\(1\)-grams
- Prediction unigrams: {I, have, socks, .}
- Reference unigrams: {In, my, dresser, I, have, socks, .}
- Total unigrams in prediction: 4
- Unigram precision: \(p_1\) = \(\frac{4}{4} = 1.0\)
\(2\)-grams
- Prediction bigrams: {I have, have socks, socks .}
- Reference bigrams: {In my, my dresser, dresser I, I have, have socks, socks .}
- Total bigrams in prediction: 3
- Bigram precision: \(p_2\) = \(\frac{3}{3} = 1.0\)
\(3\)-grams
- Prediction trigrams: {I have socks, have socks .}
- Reference trigrams: {In my dresser, my dresser I, dresser I have, I have socks, have socks .}
- Total trigrams in prediction: 2
- Trigram precision: \(p_3\) = \(\frac{2}{2} = 1.0\)
\(4\)-grams
- Prediction 4-grams: {I have socks .}
- Reference 4-grams: {In my dresser I, my dresser I have, dresser I have socks, I have socks .}
- Total 4-grams in prediction: 1
- 4-gram precision: \(p_4\) = \(\frac{1}{1} = 1.0\)
So in this case all the \(n\)-gram precisions up to \(4\) are \(1.0\). But the translation is not perfect, so how do we penalize it?
A brevity penalty is calculated. The way it is calculated is outside of the scope of this article. See the (Papineni et al., 2002) for the equation. In this case the brevity penalty is \(0.47\). The brevity penalty is multiplied with the \(n\)-gram precisions to get a final bleu score of \(0.47\).
Bleu score problems
However, the bleu score is not a perfect metric.
-
Implicit in the bleu score calculation is that the text has been tokenized. For example,
I have socks.is tokenized as[I, have, socks.]. This is not the only way to tokenize, as we’ll see later. This could lead to differences in bleu score calculation across papers. -
It does not take into consideration semantics. Let’s say the reference translation is
I have a hamburger in my bag. Candidate translation 1 isI have a sandwhich in my bag, and candidate translation 2 isI have a dolphin in my bag.They would both have the same bleu score, while we can see that candidate 2 is nonsense while candidate 1 is close. -
It was designed for English translations. Translations in other languages may not have the same “similar n-gram matches correlates with human-judgement of translation quality” property.
-
If one of the n-gram matches is 0, the bleu score is undefined since \(log(0)\) is undefined. It is usually set to 0 in this case. For example, the translation
I have socks.with referenceI have socks in my dresser.would have a bleu score of 0 since the \(4\)-gram has precision of 0. This is not a good property since it is clearly a close translation. This can be fixed by adding 1 to all n-gram precisions, but it’s not clear whether papers use this approach.
See this page for more discussion of limitations.
Regardless, bleu score is the standard for evaluating machine translations in an automated way.
Experiments and results
Now I’ll actually implement both the RNN encoder-decoder model from (Sutskever et al., 2014) and the RNN encoder-decoder model with attention from (Bahdanau et al., 2015), evaluate it on the English to French translation task of the (Bojar et al., 2014) (WMT’14) dataset, and compare results to the papers.
Dataset
In (Sutskever et al., 2014) and (Bahdanau et al., 2015), they use the (Bojar et al., 2014) (Workshop on Machine Translation a.k.a WMT’14) English-French parallel corpora dataset which contains the following:
- Europarl
- Professional translations of European parliment
- News Commentary
- Translations of news articles
- UN
- Translations from the UN meetings
- Crawled corpora
- Presumably random text on the web translated into different languages
The breakdown on the number of reported tokens per each dataset is:
| Dataset | Num. words |
|---|---|
| Europarl | 61M |
| News Commentary | 5.5M |
| UN | 421M |
| Crawled corpora | 362.5M |
They use a technique (Cho et al, 2014) to filter down to a total of 348M words for training. I did not follow this selection technique.
They use a test set of 3003 sentences for testing.
Here’s an example from the Europarl dataset:
French:
Même si cet idéal est encore loin d’être atteint, je voudrais exprimer la satisfaction de l’Union européenne de voir l’élection du Belarus au Conseil des droits de l’homme empêchée avec succès au mois de mai.
English:
Although this ideal is still far from having been achieved, I should like to express the satisfaction of the European Union that the election of Belarus to the Human Rights Council was successfully thwarted in May.
and from the News Commentary dataset:
French:
Si l’on s’inquiète de cette possibilité, l’or pourrait en effet être la couverture la plus fiable.
English:
And if you are really worried about that, gold might indeed be the most reliable hedge.
Model
I used an encoder-decoder model using a GRU in both the encoder and decoder. The encoder is bidirectional. The hidden state size in the forward and backward directions of the encoder is \(1000\) and in the decoder is \(1000\). The embedding dimensionality in both the encoder and decoder is \(1000\). Both the encoder and decoder have \(4\) layers. For attention, I used the scaled dot-product attention with \(d_v\) equal to \(1000\). The source vocab size and target vocab size were set to \(30,000\). The models with attention and without attention contains ~\(189M\) trainable params.
For comparison, (Sutskever et al., 2014) used LSTM instead of GRU. The vocab sizes were much larger at \(160,000\) for the source and \(80,000\) for the target. Their model contain \(384M\) params. To the best of my knowledge the attention model implemented is approximately equal to (Bahdanau et al., 2015), but they leave out some implementation details, so I cannot say for sure.
Training details
- I used 3 nvidia V100 GPUs to train both the model with attention and model without attention.
- Both models were trained for up to 3 epochs, or 72 hours, whichever came first. The model with attention completed ~3 epochs in 72 hours, while the model without attention completed 3 epochs.
- \(AdamW\) optimizer using cosine annealing with warmup learning rate scheduler was used. Warmup number of steps is \(2000\), min learning rate is \(6e^{-5}\) and max learning rate is \(6e^{-4}\)
- Cross entropy loss was used between the output sequence of tokens with highest probabilty and the target.
Results
Results are reported on the WMT’14 test set which contained 3003 english-french pairs.
| Model | Average BLEU score |
|---|---|
| (Sutskever et al., 2014) (Single reversed LSTM, beam size 12) | 0.306 |
| With attention | 0.297 |
| (Bahdanau et al., 2015) (RNNsearch-50*, All words) | 0.285 |
| Without attention | 0.261 |
The model with attention achieved an overall higher average BLEU score than the model without attention. The model with attention achieved a better performance than (Bahdanau et al., 2015) (RNNsearch-50*, All words), while the model without attention achieved worse performance than (Sutskever et al., 2014) (Single reversed LSTM, beam size 12).
Note that the model with attention, (Bahdanau et al., 2015) (RNNsearch-50*, All words), has a worse reported BLEU score than (Sutskever et al., 2014) (Single reversed LSTM, beam size 12).
One of the key questions we wanted to answer was whether the model without attention suffers when the input lengths increase. The following figure compares BLEU score for the model with attention vs without as the input length increases.
We are not able to reproduce a decrease in performance as the number of input tokens increases as (Bahdanau et al., 2015) and others showed. (Sutskever et al., 2014) showed that their model without attention is robust to an increase in sentence length even without attention, which is the same trend we were able to reproduce.
Random examples
Let’s look at a few randomly chosen translations from the test set.
example 1
| Input | With attention Prediction | Without attention Prediction | Target |
|---|---|---|---|
| California planners are looking to the system as they devise strategies to meet the goals laid out in the state’s ambitious global warming laws. | Les planificateurs de la Californie se tournent vers le système lorsqu’ils élaborent des stratégies pour atteindre les objectifs énoncés dans les lois ambitieuses de l’État sur le réchauffement planétaire. | Les planificateurs californiens se tournent vers le système pour mettre au point des stratégies visant à atteindre les objectifs énoncés dans la législation ambitieuse du réchauffement de la planète. | Les planificateurs de Californie s’intéressent au système puisqu’ils élaborent des stratégies pour atteindre les objectifs fixés dans les lois ambitieuses de l’État sur le réchauffement climatique. |
While I don’t speak French, plugging in both predictions into Google Translate produces:
With attention
California planners are turning to the system as they develop strategies to meet the goals set out in the state’s ambitious global warming laws.
Without attention
California planners are looking to the system to develop strategies to meet goals set out in ambitious global warming legislation.
Both are close, but the translation with attention is better as it produces the goals rather than goals and also the translation without attention misses the important phrase the state’s. Also the word legislation is awkward and laws is better.
example 2
| Input | With attention Prediction | Without attention Prediction | Target |
|---|---|---|---|
| “Despite losing in its attempt to acquire the patents-in-suit at auction, Google has infringed and continues to infringe,” the lawsuit said. | “Malgré la perte dans sa tentative d’acquérir les brevets en cours d’enchère, Google a enfreint et continue de violer”, a déclaré la poursuite. | “En dépit de sa perte dans l’acquisition des brevets en cours aux enchères, Google a enfreint et continue de violer”, a-t-il poursuivi. | « Bien qu’ayant échoué dans sa tentative d’acquérir les brevets en cause au cours des enchères, Google a violé et continue à violer lesdits brevets », ont indiqué les conclusions du procès. |
With attention
“Despite losing its bid to acquire the patents in the auction, Google has infringed and continues to infringe,” the suit said.
Without attention
“Despite its loss in the pending patent auction, Google has infringed and continues to infringe,” he continued.
We see a similar pattern as before. The model with attention pretty much gets it right, while the model without attention adds the word pending to patent auction which is incorrect, and ends with he continued which is incorrect and should be the lawsuit said.
example 3
| Input | With attention Prediction | Without attention Prediction | Target |
|---|---|---|---|
| He also said that a woman and child had been killed in fighting the previous evening and had been buried. | Il a également déclaré qu’une femme et un enfant avaient été tués dans les combats de la soirée précédente et avaient été enterrés. | Il a également déclaré qu’une femme et un enfant avaient été tués au cours de la nuit précédente et avaient été enterrés. | Selon lui, une femme et son enfant ont été tués par les combats de la veille et ont été enterrées. |
With attention
He also said that a woman and a child had been killed in the fighting the previous evening and had been buried.
Without attention
He also said that a woman and a child had been killed during the previous night and had been buried.
The model with attention gets it right while the model without attention misses the important phrase in the fighting and adds the slightly awkward during.
Looking at attention weights
Attention, as described above, give the decoder the ability to give different weights to different tokens in the input. We can inspect these weights to understand better which input tokens each decoding timestep is “paying attention to”.
Above is a figure showing 4 randomly chosen examples from the WMT’14 test set which have input lengths between 10 and 20 tokens. We can see that the attention weights are mostly linear. For example in the top left subplot we can see that at timestep \(1\), the model most strongly pays attention to the english token _But to produce the french token _Mais, and at timestep \(2\) the model most strongly pays attention to _why to produce the french token _porquois.
However there are deviations from this. For example in the bottom left subplot we can see that the english phrase phone calls gets translated to the french appels téléphoniques, which literally translates to calls phone, and we can see that when outputting appels, the input token calls is most strongly paid attention to, while when outputting téléphoniques, phone is most strongly paid attention to.
Sometimes, we can see that a given token in the input is paid attention to by multiple timesteps in the decoder. For example, in the bottom right subplot we can see that the input returned is paid attention to by the phrase les gens sont revenus or in english the people returned. So in addition to paying attention to revenus when outputting the literal translation returned, the model is paying attention to returned when outputting the entire phrase les gens sont revenus. This shows that the surrounding phrase is helpful here.
We can see another case where the model outputs multiple tokens which maps to a single input token. In the top left subplot the output tokens, _l, ‘, _autorité all pay attention to the input token _authority, and which is a good property since authority gets split up into the 3 french tokens l, ‘, _autorité.
Failure mode examples
It’s useful to look at examples where the model performs poorly.
| Input | With attention Prediction | Without attention Prediction | Target |
|---|---|---|---|
| I should say that I am rather sociable and have a job with responsibilities. I laugh and sing, I go out, I’m a grandmother, I have lots of friends, but my heart and my soul belong to him. I never talk about him except with my son, and I never go to the cemetery. | Je dois dire que je suis plutôt sociable et j’ai un travail avec des responsabilités. | Je dois dire que je suis assez sociable et qu’il est un homme qui a des devoirs, je rentre et j’essaie de chanter, je suis une grand-mère, j’ai beaucoup d’amis, mais mon cœur et moi-même l’âme, je n’en parle qu’à mon fils, mais | Je tiens à préciser que je suis sociable avec un métier à responsabilité, je ris et je chante, je sors, je suis grand-mère, j’ai plein d’amis, mais mon cœur et mon âme lui appartiennent et je ne parle jamais de lui sauf avec mon fils, et je ne vais jamais au cimetière. |
Interesting, it looks like the model is having trouble because there are multiple sentences separated with “.”, which is not common in the dataset. Each sentence is supposed to be split. The model has trouble with this and stops at the first period.
This is a failure mode that would definitely need to be worked on, possibly by splitting on period and translating each sentence separately.
Implementation details
I’ll now go through the nitty-gritty of some of the implementaton details.
Tokenization
In (Bahdanau et al., 2015), tokenization was treated as an after-thought. They say
After a usual tokenization, …
However I soon realized that tokenization is an important topic and can influence the model in many ways. Curious what SOTA LLMs use, I found that it is more common to use an algorithm called Byte-pair encoding algorithm, for example as discussed in (Radford et al., 2019).
Byte-pair encoding algorithm
As mentioned previously, tokenization is the way by which we feed the inputs to the model. Unfortunately, there is no way currently to feed the inputs directly to the model. The inputs must be chunked into discrete tokens.
Traditionally, inputs might be tokenized by breaking up into words or characters.
For example in the sentence
I have socks.
it might be tokenized as ['I', ' ', 'have', ' ', 'socks', '.']
but it could also be tokenized as ['I', ' ', 'h', 'a', 'v', 'e', ' ', 's', 'o', 'c', 'k', 's', '.']
The “vocabulary” is then the set of possible tokens. One problem is that not every word encountered might be represented in the vocabulary. Traditionally, rare words or given the token “UNKOWN” so as to limit the vocabulary, and to handle tokens not seen in the training set. However this is not great; we’d like the model to be able to handle anything without defaulting to an UNKNOWN token.
Splitting on words is not great as that introduces a bias. In deep learning we like the model to learn the raw signal without human intervention and splitting on words is somewhat of a human intervention. Splitting on characters is better, but introduces other problems as discussed in (Radford et al., 2019).
One idea is to feed the model UTF-8 bytes directly. However, for each character, 1-4 bytes are used in UTF-8. We would have a vocabulary of size 256 (\(2^8\) possible tokens can be modeled with a single byte). In this case the input size would explode in some cases since for each character we are using 1-4 tokens. For english tokens just a single byte is used but for characters in other languages and special tokens such as math, up to 4 bytes are used. This is a problem computationally, and so we would like the inputs to be somewhere on the spectrum of “word-level tokenization”, “character-level tokenization”, and “UTF-8 byte level representation”.
(Radford et al., 2019) (GPT-2 paper) adopted the BPE (byte-pair encoding) algorithm, which allows for a middle ground between these representations, and solves the issue of being able to model any possible character.
The BPE algorithm in short converts a “training set”, which is possibly a sample of text used to train for the problem we’re working on, or a completely different set of text, to UTF-8 bytes. As mentioned, this is a vocabulary of size 256. We want to expand the vocabulary.
Then, the most common pairs of bytes are merged. These merges get added to the vocabulary.
This continues until the vocabulary gets to a certain size, which is a hyperparameter.
Note that this solves the problems mentioned above. We are using a byte-level representation, but for common sequences of bytes, such as common words, we are representing those as a single token. For characters not in the training set, those are left as individual bytes, which can be achieved by using byte_fallback=True in the sentencepiece algorithm.
Side note: The BPE algorithm was originally developed as a compression algorithm in 1994.
Implementation of BPE
OpenAI has released their BPE algorithm but it can only be used for inference.
The sentencepiece algorithm is similar to the above implementation, and was used for Meta’s LLama 2. It has a very efficient training implementation, so this is what I used.
See the excellent overview of BPE and sentencepiece by Andrej Karpathy
Using multiple GPUs
To train on multiple GPUs, the torch.nn.parallel.DistributedDataParallel package in pytorch was used. Since it was the first time using it, I’ll explain briefly how it works.
At a high level, the model is duplicated across the GPUs, each running in a separate process. When the backward pass is completed, the gradients are synced with a master process. The updated gradients then sync with the other processes.
To use DistributedDataParallel, we just need to wrap the pytorch model in DistributedDataParallel:
model = DistributedDataParallel(model, device_ids=[...])
To make use of DDP, we can use the torchrun command line utility in pytorch. It assists in launching multiple processes and setting environment variables.
Important envionrment variables are RANK and LOCAL_RANK. RANK is the global identifier for the process, and LOCAL_RANK is the local identifier for a process. torchrun can launch processes across machines, in which case these will be different, but on the same machine they will be the same. device_ids should be the LOCAL_RANK.
Note: Only log and check validation performance from the master process (the one where RANK == 0)!
Padding
During development of the model I experienced a strange issue that took all day to debug. I’ll first describe why padding is needed, the issue I encountered, and then the solution.
When training we construct minibatches to parallelize the computation. We must pass a single tensor to the model, and so all sequences must be made to be the same length. This means that if the sequences are different lengths, then we need to add a special token to any sequence which is shorter than the longest sequence.
Let’s say we had this minibatch:
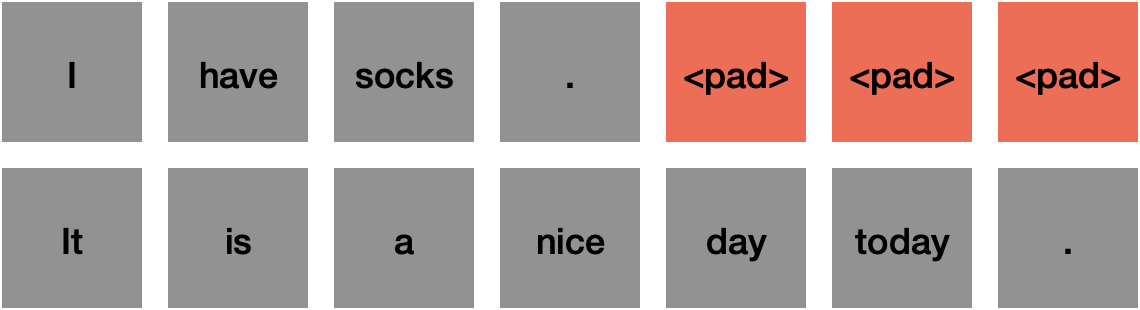
The 3 padding tokens in the 1st sequence are required because the 1st sequence is shorter than the 2nd sequence.
the issue
What I encountered is that when I passed the 1st sequence as is with the 3 padding tokens through the encoder-decoder, the output translation was one thing. But when I removed the padding tokens, and just passed the sequence by itself without padding tokens, I got a totally different translation.
This to me was a bad sign. The model should not be sensitive to the padding tokens; they should be ignored. Their only purpose should be to make the sequences in the minibatch the same length and shouldn’t have any meaning.
the solution
Padding affects the model in a few ways.
The 1st way is when we encode the input sequences in the minibatch, the RNN must iterate through each token in the sequence, including the pad tokens. We would like for the encoder to learn that the pad tokens are irrelevent, which is what I thought would happen with enough data. But clearly this was not the case. How can we force the encoder to ignore the pad tokens?
It turns out in pytorch there is function to force RNNs to ignore the pad tokens.
packed_embedded = torch.nn.utils.rnn.pack_padded_sequence(
input=input,
lengths=input_lengths,
batch_first=True,
enforce_sorted=False
)
Given the tensor with the pad tokens, and the lengths of each sequence in the tensor, torch.nn.utils.rnn.pack_padded_sequence will construct a PackedSequence object which any RNN module in pytorch knows how to take as input. The RNN will know to ignore the pad tokens.
The 2nd way is the loss function. In the cross-entropy loss we are comparing the predicted token with the actual token for a minibatch of predicted and actual sequences, e.g.
loss = criterion(
decoder_outputs.reshape(batch_size * T, C),
target_tensor.view(batch_size * T)
)
What happens if the sequences are padded with a bunch of pad tokens? If we evaluate the loss where a significant number of decoder_outputs are pad tokens and target_tensor are pad tokens, then the loss will be biased towards the pad tokens. We want the loss to reflect the actual tokens, and not the pad tokens. It turns out that CrossEntropyLoss supports ignore_index which will ignore a specific index in the loss calculation; in this case it should be set to the <pad> token.
The 3rd way is the attention mechanism when calculating the attention weights. We don’t want the model to pay attention to the pad token.
If we look again at the equation for attention:
\[attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V\]We want \(V\) to be 0 where the padding tokens are. To do that we just need to set the scores \(QK^T\) to \(-{inf}\) where the padding tokens are.
scores = torch.bmm(query, keys.transpose(1, 2)) / math.sqrt(Dq)
scores = scores.masked_fill(mask.unsqueeze(1), float('-inf'))
where \(mask\) is \(1\) where the pad tokens are.
does it work?
Hopefully all this effort to ignore the pad token works and the model is insensitive to the number of pad tokens, which wasn’t the case when I didn’t ignore the pad token in the RNN encoder and in the attention layer.
In the following example we randomly sample a test example, check the output with no padding and compare it with the output with a randomly chosen number of pad tokens appended.
input: Moore told reporters that the initial autopsy indicated Johnson died as a result of "positional asphyxia."
output with no pad tokens appended to input == output with 42 pad tokens appended to input True
===========
input: "The alarms went off one after the other as it took reinforcements to deal with the building, because the buildings here are close together," explained France Loiselle, spokesperson for the Quebec fire service.
output with no pad tokens appended to input == output with 13 pad tokens appended to input True
===========
input: Rehousing Due to Rats Causes Strife in La Seyne
output with no pad tokens appended to input == output with 29 pad tokens appended to input True
===========
input: I see her eyes resting on me.
output with no pad tokens appended to input == output with 26 pad tokens appended to input True
===========
input: Moreover, Kiev needs liquid assets to pay for its gas imports from Russia, which accuses it of not having paid a bill of 882 million dollars.
output with no pad tokens appended to input == output with 3 pad tokens appended to input True
===========
Great, the model seems to be ignoring the pad tokens!
Sequence generation
When we’re producing the output sequences it turns out that there are multiple ways to go about it and some are better than others.
greedy search
The simplest is called “greedy search” and involves just selecting the token with the highest predicted probability of being the correct token at each timestep.
I thought this would be sufficient, as the model is being optimized to learn which is the correct token at each timestep \(t\) given the previous \(t-1\) tokens.
However, it turns out that this can produce suboptimal, awkwardly phrased, or strange outputs. It can select a bad token at timestep \(t\) and then this creates a bad sequence going forward.
beam search
A solution to this is to use “beam search”. (Sutskever et al., 2014) and (Bahdanau et al., 2015) both use beam search to produce the output sequences.
At each timestep \(t\), beam search will choose the \(B\) most likely next tokens, as well as store the following things:
- the decoder hidden state at timestep \(t\)
- the generated sequence at timestep \(t\)
- The log-likelihood of the sequence
We start by choosing \(B\) most likely tokens to start the sequence. Then for each of these sequences, we select the \(B\) most likely next tokens, producing \(B^2\) possible sequences. From this list of possible sequences, we choose the \(B\) most promising by comparing the log-likelihood of each sequence and choosing the \(B\) sequences with the highest log-likelihood. We complete the search once all \(B\) beams terminate with an end of sentence token or when we’ve done a certain number of iterations of search, whichever comes first.
Impact of beam search
The above results shown figure 10 are using beam search using a beam width of 10.
We can see from the figure below that beam search in general improves performance compared to greedy, but also produces a translation of equivalent quality to greedy more generally and sometimes worse. Beam search also takes significantly longer to run.
beam search example
As an example, let’s consider the following input:
The theatre director immediately began an evacuation procedure and called the fire brigade to check out a suspicious smell.
This has the ground truth french translation:
Immédiatement, le directeur de l’établissement a fait procéder à l’évacuation de la salle et a prévenu les pompiers pour une odeur suspecte.
The greedy search prediction is:
Le directeur du théâtre a immédiatement entrepris une procédure d’évacuation et a appelé la brigade de pompiers pour vérifier une odeur suspecte.
Let’s see what beam search produces.
For this example I am using a beam-size \(B\) of \(2\).
Beam search starts off predicting the 1st token:
iteration 1
| Sequence | log-likelihood |
|---|---|
| 0.0 | |
| ’ | -19.966 |
It starts off predicting start of sentence and an apostrophe token.
Then, for each of these beams, it predicts \(B\) next tokens:
iteration 2
| Sequence | log-likelihood |
|---|---|
| Le | -0.387 |
| La | -3.325 |
| ’ Le | -20.716 |
| ’ La | -22.956 |
For each of the previous 2 beams, we search for the next token. Le is the most likely, while La is second most likely. We select these 2 beams and continue expanding both.
iteration 3
| Sequence | log-likelihood |
|---|---|
| Le directeur | -0.560 |
| Le chef | -4.279 |
| La directrice | -3.885 |
| La direction | -5.589 |
Let’s see what happens next.
iteration 4
| Sequence | log-likelihood |
|---|---|
| Le directeur du | -1.102 |
| Le directeur de | -1.667 |
| La directrice du | -4.574 |
| La directrice de | -5.007 |
iteration 5
| Sequence | log-likelihood |
|---|---|
| Le directeur du théâtre | -1.267 |
| Le directeur du secteur | -5.419 |
| Le directeur de théâtre | -2.450 |
| Le directeur de la | -2.565 |
We can see how beam search is trying out different possibilities for the next token and adjustment the likelihood after expanding each of the most likely \(B\) beams \(B\) times.
It continues like this for 28 iterations. The final list of beam candidates are:
| Sequence | log-likelihood |
|---|---|
| Le directeur du théâtre a immédiatement entrepris une procédure d’évacuation et a appelé la brigade d’incendie pour vérifier une odeur suspecte. | -12.367 |
| Le directeur du théâtre a immédiatement entrepris une procédure d’évacuation et a appelé la brigade d’incendie pour vérifier une odeur suspecte de | -19.076 |
| Le directeur du théâtre a immédiatement entrepris une procédure d’évacuation et a appelé la brigade d’incendie à vérifier une odeur suspecte. | -12.813 |
| Le directeur du théâtre a immédiatement entrepris une procédure d’évacuation et a appelé la brigade d’incendie à vérifier une odeur suspecte de | -12.813 |
We can see that 2 of the sequences are incomplete, but because \(B=2\) of the sequences are complete, beam search terminates. This is a bias of beam search that it prefers shorter sequences.
Handling unknown tokens
In previous attempts at language modeling, a fixed size vocabulary would be constructed and used for training. What happens when the model sees an unknown token at test time? What should the model do? The model would typically just output a special <UNK> token, standing for unknown. But this is not useful. We don’t want to see that. When using chatgpt for example, we don’t want to see <UNK> in the output, but what if a user enters something it has never seen before?
We mentioned before in the section on tokenization that the initial vocabulary when using the sentencepiece algorithm with byte_fallback=True is that the initial vocabulary contains all UTF-8 bytes. When an unexpected token is encountered in this scenario, the sentencepiece algorithm will break down the token into its UTF-8 bytes, and since each UTF-8 byte is part of the vocabulary, the model will not need to output the <UNK> token.
When we use the byte-pair encoding algorithm, we break up the sequence into familiar chunks, if familiar chunks exist. We can do this for the word suspecte which means suspicious. It breaks up this word into 2 tokens, since the word suspecte by itself wasn’t common enough in the tokenizer training set.
In code:
target_tokenizer.processor.encode("suspecte", out_type=str)
['▁suspec', 'te']
These 2 tokens were common enugh in the tokenizer training set to be included as tokens.
The underscore in “▁suspec” seems strange at first; sentencepiece encodes “word boundaries” or starts of words with “_”.
To my surprise, I didn’t find any examples of byte_fallback being activated in the test set. Meaning that every word can be broken up into chunks that are known vocabulary tokens.
Let’s take a sequence with a rather rare looking word “Ikhrata”, which is someone’s surname, from the test set:
“It is not a matter of something we might choose to do,” said Hasan Ikhrata, executive director of the Southern California Assn. of Governments, which is planning for the state to start tracking miles driven by every California motorist by 2025.
This word is not in the training set. How does the tokenizer handle this?
source_tokenizer.processor.encode("Ikhrata", out_type=str)
['▁I', 'kh', 'ra', 'ta']
It breaks up the word into familiar chunks, known vocabulary tokens. This is the advantage of using a tokenization algorithm like sentencepiece, compared to just breaking up sequences into words. The word “Ikhrata” would be unknown and we would not know what to do with it.
What is the model’s output?
« Il ne s’agit pas d’une chose que nous pourrions choisir de faire », a déclaré Hasan Ikherata, directeur exécutif de la Southern California Assn. of Governments, qui prévoit que l’État commencera à suivre les kilomètres parcourus par tous les automobilistes de la Californie d’ici 2025.
“Ikhrata” was not found in the training set, and the model output “Ikherata”, which is not good.
However, this shows that we can output something rather than <UNK>.
Mixed precision training
The default datatype for network operations in pytorch is torch.float32.
However, it turns out that most deep learning operations don’t require this much precision, and float16 would suffice. But not all operations can use the lower precision, which is why pytorch and the GPU know how to do some operations using float32 and some with float16. That is why it is called mixed precision.
This is a good thing that we don’t need to always use float32 since float16 takes up less memory than float32, which allows the GPU to access the data quicker and allows us to use larger batch sizes. See this article which shows that using mixed precision training achieves the same accuracy as float32 and shows that mixed precision training ran 2-5 times faster.
In my experiments using the Nvidia V100 GPUs, training on float32 took 1.80s/batch while training with float16 took 0.99s/batch, which matches what the PyTorch article above reported.
This is great, since it means that training time is cut down by half.
Conclusion
We implemented an RNN model without attention similar to (Sutskever et al., 2014) and a model with attention similar to (Bahdanau et al., 2015) and found that the model with attention has better overall performance than the model without attention as evaluated by the BLEU score on the 3003 test set examples in the WMT’14 dataset. However, (Bahdanau et al., 2015) reports a steep decrease in BLEU score as the sentence length increases, which we were not able to reproduce. Our results are in line with (Sutskever et al., 2014) which reported that the model without attention is robust to sentence length, but the paper that introduced attention is seen as a “paradigm shift” paper that introduced attention, so the community saw value in the attention mechanism though the reported performance in the paper is not as good as previous papers.
Researchers ran with the idea of attention, and developed the transformer architecture, which forms the backbone of SOTA “language models” such as the GPT series.
Also of note that at the time, non-deep-learning based methods such as Moses, showed better performance on the translation task, but clearly the community invested more effort in deep learning based methods. The transformer model paid off and is significantly more influential than just in doing translation, which Moses is only capable of doing.
Importantly, the problem of translation is used, as these papers were focused on, but learning to translate is actually similar to learning to take in an arbitrary sequence and output an arbitrary sequence, which for example chatbots, image generators, video generators, etc need to do. So the applications of this research are more applicable than just to the problem of translation.
Next, we’ll build on language models and implement a transformer model rather than an RNN model.
References
References
- Neural Machine Translation by Jointly Learning to Align and TranslateIn 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings, 2015
- Sequence to sequence learning with neural networksIn Proceedings of the 27th International Conference on Neural Information Processing Systems - Volume 2, Montreal, Canada, 2014
- On the Properties of Neural Machine Translation: Encoder–Decoder ApproachesIn Proceedings of SSST-8, Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation, Oct 2014
- Language Models are Unsupervised Multitask LearnersIn , Oct 2019
- Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine TranslationIn Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing, EMNLP 2014, October 25-29, 2014, Doha, Qatar, A meeting of SIGDAT, a Special Interest Group of the ACL, Oct 2014
- Attention is all you needIn Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, California, USA, Oct 2017
- BLEU: a method for automatic evaluation of machine translationIn Proceedings of the 40th Annual Meeting on Association for Computational Linguistics, Philadelphia, Pennsylvania, Oct 2002
- Findings of the 2014 Workshop on Statistical Machine TranslationIn Proceedings of the Ninth Workshop on Statistical Machine Translation, Jun 2014
Enjoy Reading This Article?
Here are some more articles you might like to read next: